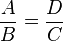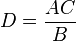Sumas Iguales

Objetivo: Relacionar combinaciones básicas de adición de cuatro sumandos distintos que tienen sumas iguales

Materiales: - 40 naipes de cartulina construidos según el modelo

                   - Papel y lápiz

Reglas:

1- Participan de 2 a 4 estudiantes que juegan por turnos

2- El juego consiste en buscar la pareja de distinto color que le corresponde a cada carta de acuerdo a la siguiente regla: "tener que sumar igual"

3- Se reparten 6 cartas por jugador. Las sobrantes se colocan boca abajo en el centro de la mesa

4- El primer jugador toma la primer carta del mazo. Si logra hacer pareja con las que tiene en la mano, debe entregarlas para su verificación a un juez previamente asignado por el grupo

5- Si la pareja corresponde se anotará un punto a favor del jugador que la obtuvo, de lo contrario se le anota un punto en contra que le será sustraído de su computo total, al finalizar el juego

6- El juego finaliza cuando se acaban las cartas de la mesa

7- Gana el jugador que obtuvo mayor puntaje

Descripción del material

- El mazo consta de 40 naipes de 6 x 9 confeccionados de cartulina según el modelo

- Cada naipe tiene cuatro números del 0 al 15 que deberán ser sumados

Ejemplo de parejas de Naipes

No dudes en escribir cualquier duda o comentario.

Sumando con Cubos

Objetivo: Reforzar el concepto de adición con reagrupamiento
Materiales:
- Un dado numerado del 1 al 6
- Un cubo con una de estas letras en cada cara: S, U , M , A , N, D, O.
- 15 fichas para cada jugador (un color diferente por cada participante)
- Un tablero de juego con 6 x 6 casillas con ejercicios de adición de dos números de dos                      dígitos, con o sin reagrupamiento en cada espacio (a continuación se presenta un modelo)

Reglas:

1. En este juego pueden participar de 2  4 personas

2. Cada jugador de acuerdo a su turno lanza el dado y el cubo con letras. Obtendrá un par ordenado formado por un número y una letra que indicará el lugar en el tablero del ejercicio por resolver, ejemplo (3 , M)

3. El jugador deberá realizar la adición mostrando la solución obtenida en cada caso

4. Si la respuesta obtenida es correcta, el jugador coloca una de sus fichas en el lugar correspondiente

5. Si el otro jugador al lanzar los dados obtiene el mismo par ordenado que otro jugador, puede capturar la ficha de ese jugador y resolver el ejercicio correspondiente

6. El ganador es el jugador que logra 6 de sus fichas en linea horizontal, vertical o diagonal


Variaciones

- Este juego puede extenderse a un ámbito numérico mayor, o usar ejercicios de sustracción, multiplicación o división o una mezcla de estas operaciones

- Los participantes podrán hacer sus propios tableros, eligiendo conjunto de ejercicios que deseen revisar para hacer otros tableros

    No dudes en comentar

Construcción de la ecuación de la recta

Hay dos maneras de definir una recta única

• Dados dos puntos donde pasa la recta
• Dado un punto donde pasa y la pendiente de la recta

   En función de los datos que tengamos en cada caso, vamos a aplicar dos métodos diferentes para saber la ecuación de la recta que nos definen por cualquiera de esas dos maneras. 

  Construcción de la ecuación de la recta, conociendo un punto y la pendiente

   Veamos un ejemplo concreto: 

      Encontrar la ecuación de la recta que pasa por el punto (1;0) y tiene por pendiente el valor -2

   La manera de hallar la ecuación de la recta es la siguiente

   Recordemos que la ecuación general de la recta es  y = a.x +b

    Donde el valor de "a" es la pendiente y "b" es la ordenada al origen

    Sigamos un razonamiento para hallar la ecuación solicitada

    Reemplazamos el valor "a" (correspondiente a la pendiente) ya que el mismo es dato a = -2

    Lo que nos falta ahora definir es el valor de "b" (la ordenada al origen)

    Podemos seguir el siguiente método

   Partimos nuevamente de la ecuación general de la recta y=a.x + b

   Reemplazamos a por (-2) con lo que queda la recta y = -2 x + "b"

   Reemplazamos la "x" y la "y" por las coordenadas del punto que nos dieron y despejamos "b" 

   (recuerda que cuando nos dan las coordenadas de un punto, la primera corresponde al valor de x y la segunda a y) 

   

  Construcción de la recta conociendo dos puntos que pertenecen a ella

   Veamos un ejemplo concreto: Hallar la recta que pasa por los puntos (1 ; -2) y (2 ; 3)

   Partiremos de la Ecuación General de la Recta

   La manera de resolver que plantearemos es  diferente, ya que lo resolveremos utilizando sistemas de ecuaciones, así de esta manera evitamos tener que recordar cualquier tipo de formula. 

   Reemplazaremos las "x" y "y" correspondientes a las coordenadas de cada punto; con lo cual quedarían dos ecuaciones con dos incógnitas (en este caso, las incógnitas serán la pendiente y la ordenada al origen "a" y "b")

   

   Armamos el sistema de ecuaciones 

   Para resolverlo podemos recurrir a cualquiera de los métodos correspondientes para resolver Sistemas de Ecuaciones.

   Nosotros en este caso particular utilizaremos el Método de Sumas y Restas

   Preparamos las ecuaciones para sumarlas o restarlas. En este caso, vamos a restarlas

   Ahora a partir de este valor estamos en condiciones de calcular el valor de b

   Como siempre esperamos que la publicación sea de ayuda y espero sus comentarios 

   

    

Teorema de Tales

  Para "entrar" en tema comenzamos observando el siguiente vídeo.

   Lo obtuve del canal Germanflaco de youtube 

   

   

   Un poco de historia relacionado al Teorema 

   Según la leyenda (relatada por Plutarco), Tales de Mileto en un viaje a Egipto, visitó las pirámides de Guiza, Keops, Kefrén y Micerino. 
   Admirado ante imponentes monumentos de esta civilización, quiso saber su altura. De acuerdo a la leyenda, trató este problema con semejanza de triángulos (y bajo la suposición de que los rayos solares incidentes eran paralelos), pudo establecer una relación de semejanza entre dos triángulos rectángulos, por un lado el que tiene por catetos (C y D) a la longitud de la sombra de la pirámide (conocible) y la longitud de su altura (desconocida), y por otro lado, valiéndose de una vara (clavada en el suelo de modo perfectamente vertical) cuyos catetos conocibles (A y B) son, la longitud de la vara y la longitud de su sombra. Realizando las mediciones en una hora del día en que la sombra de la vara sea perpendicular a la base de la cara desde la cual medía la sombra de la pirámide y agregando a su sombra la mitad de la longitud de una de las caras, obtenía la longitud total C de la sombra de la pirámide hasta el centro de la misma.

   Como en triángulos semejantes, se cumple que  , por lo tanto la altura de la pirámide es  , con lo cual resolvió el problema.

   Ahora puedes observar que la relación antes mencionada en la siguiente construcción. 
   Recuerda que puedes desplazar todos los puntos rojos, observa como las medidas se modifican, mientras las razones permanecen invariantes.  

     Si deseas puedes dejar tu comentario a continuación 

Analizaremos la multiplicación de dos números complejos (de forma gráfica)

   En publicaciones anteriores hemos explicado como se realiza la multiplicación de dos números complejos, si ellos estaban expresados de forma binomica, como par ordenado o polar.

   Recordemos a partir de un ejemplo como se realizaba la multiplicación de dos números complejos:

    Retomemos especialmente la multiplicación de dos números complejos si ellos están expresados de forma polar y comenzaremos recordando ciertos aspectos importantes para comprender posteriormente la explicación.

   (Si consideras que necesitas información referida a las distintas formas de expresar un número complejo o a la multiplicación en si misma, puedes recurrir a los siguientes enlaces)  

http://sabrinamatematica.blogspot.com.ar/2013/03/multiplicacion-de-numeros-complejos.html
http://sabrinamatematica.blogspot.com.ar/2013/04/diferentes-formas-de-expresar-un-numero.html
   

   Expresemos de manera polar los números complejos dados: 

   Reemplazamos los valores obtenidos en la fórmula expresada anteriormente

   Quedando demostrado lo que en forma gráfica fue hallado.

Tangram

El Tangram es un juego chino muy antiguo, compuesto por 7 (siete) figuras geométricas.
El objetivo es reproducir una figura dada utilizando todas las piezas, sin dejar espacio entre ellas o superponerlas. 
Para intentar reproducir los números 2 y 0 (recuerda que debes utilizar todas las piezas en cada caso) 
Ultima aclaración antes de jugar. Puedes girar las piezas moviendo el punto rojo.




Si deseas alguna figura en particular deja tu comentario.

Dodecaedro Regular

   Un dodecaedro es un poliedro de doce caras, las mismas son pentágonos regulares. 
   Es uno de los llamados sólidos platónicos.

  A continuación se presenta un vídeo donde se pueden observar algunas características especificas y la construcción de un Dodecaedro utilizando para ello el programa Cabri 3D 

   Gracias por visitar las publicaciones que realizo. A continuación puedes dejar tu comentario o consulta. 

Triángulos Rectángulos

  En el siguiente power point se desarrollan cuales son los elementos que componen un triángulo rectángulo, las razones que presentan dichos elementos y cuales son los pasos a seguir frente a la necesidad de estimar algunos de ellos frente a su ausencia.

  

Resolución de triangulos rectangulos from Sabrina Dechima

   Espero que la publicación sea de ayuda y como siempre les digo: Aguardo sus comentarios o consultas

Resolución de Triángulos Rectángulos

Repaso del Teorema de Pitágoras

 Recordemos que la Hipotenusa SIEMPRE es el lado más largo (opuesto al ángulo recto) y  los catetos son los dos lados que forman el ángulo recto.

  Esté teorema nos permite calcular el tercer lado de un triángulo rectángulo, conociendo cual es el valor de los dos restantes.

   Veamos un ejemplo concreto:

   Supongamos que tenemos como dato que los catetos miden 3 cm y 4 cm respectivamente.
 ¿Cuál será la medida de la Hipotenusa?

  La Trigonometría es la parte de la matemática que estudia las relaciones entre los lados y los ángulos de los triángulos 

   Analicemos las relaciones presentes en los Triángulos Rectángulos

• Llamamos Hipotenusa al lado más largo del triángulo
• Llamamos Cateto Opuesto, al lado opuesto al ángulo considerado
• Llamamos Cateto Adyacente, al lado Adyacente al ángulo considerado 

     A partir de los tres lados y el ángulo, surgen tres relaciones muy importantes:

   Ahora bien, ¿Para qué pueden ser usadas las fórmulas mencionadas anteriormente?

   Las fórmulas anteriores son muy útiles ya que me permiten resolver cualquier triángulo rectángulo si conocemos: un lado y un ángulo o dos lados y a partir de estos datos hallar los valores restantes.

   Veamos un  ejemplo y su resolución (en este caso tenemos como dato un lado y un ángulo)



Ahora calcularemos un ángulo

   Tenemos como dato dos lados.

 

  (Al despejar el Coseno, pasa al otro lado como ArcCoseno, ya que es su función inversa)

   Para calcular el ArcCoseno de 0,6 con la calculadora: presionamos la tecla "Inv", luego Cos, o,6 y por ultimo = 

   Alfa es un ángulo y no puede poseer una amplitud con coma, es por ese motivo que debemos expresar su valor en Sistema Sexagesimal (grados, minutos y segundos). Para ello, presionamos las teclas Inv y posteriormente °´´´. Obteniendo de esa manera el valor indicado.

   Por su parte para hallar el ángulo restante, procederemos por el camino más directo; y para ello nos valdremos de una de las propiedades fundamentales de los triángulos: "En todo triángulo la suma de sus ángulos interiores es 180°"

   De está manera estimamos beta: 180° - 90° - 53 7´21´´ 

   De está manera obtenemos que beta = 36° 52´49´´  

   Como siempre les digo: espero que sea de ayuda la publicación y espero sus comentario o sugerencias. 

Expresiones decimales

     Al efectuar la división entre el numerador y el denominador de una fracción, se obtiene una expresión decimal, que puede ser exacta o periódica 

     Es exacta cuando al simplificar la fracción hasta hacerla irreducible, los factores primos del denominador son solamente 2 ó 5

     Si entre los factores primos del denominador aparece algún número que no es 2 ó 5, la fracción puede escribirse como una expresión decimal periódica. 

     Las expresiones decimales periódicas pueden ser puras o mixtas.

   Método práctico para expresar como número racional

una expresión periódica 

   El denominador surge de escribir un 9 por cada cifra decimal periódica y un 0 por cada cifra decimal no periódica 

   El numerador se forma considerando toda la expresión decimal "como si no tuviera coma", retándole la parte que "no tiene arquito" 

   Veamos un ejemplo concreto.   Expresar cómo número racional la expresión 

   

El Multiplicador (Juego para repasar las tablas)

   Los jugadores se alternaran para anticipar el resultado de una multiplicación.
       
Materiales necesarios:

• Dos jugadores 
• 1 Tablero, como el que figura a continuación
• 2 grupos de fichas de colores (uno para cada jugador)
• Los números del 1 al 9 (dos de cada uno)  

Procedimiento

1° Se elige quien comienza el juego

2° Este jugador, debe elegir dos números (pudiendo ser iguales) anticipar el resultado de su producto

3° Si la respuesta es correcta coloca una ficha de su color en el lugar correspondiente al producto realizado. Pasa el turno al otro jugador. Si la respuesta es incorrecta, pierde el turno.

4° Gana el jugador que logra ubicar cuatro fichas correspondiente a su color en fila (horizontal, vertical o diagonal)

Potencia de un Número Complejo (en forma Polar)

   Calcular las potencias de números imaginarios no es tarea sencilla, pero es bueno tener estrategias que puedan facilitar esta tarea.

   Una de las estrategias que se puede utilizar es expresar el número complejo de forma polar, ya que esto como verán a continuación facilita enormemente la tarea.
 
   Si no recuerdan cuales son los pasos a seguir les dejo el link donde pueden hallar la explicación paso a paso:   http://sabrinamatematica.blogspot.com.ar/2013/04/diferentes-formas-de-expresar-un-numero.html

   Volviendo a la idea original de la publicación, ¿Cómo se estima la potencia de un número complejo expresado en forma polar?

   Para calcular una potencia "N" de un Número Complejo en Forma Polar, elevamos el Módulo a la potencia "N", y multiplicamos el Argumento por "N"
 

   Veamos un ejemplo concreto donde se aplica la formula anterior

   ¿Pero que sucede si el Complejo no esta expresado de forma Polar ? 

   Lo que se debe hacer es primeramente cambiar la expresión y luego proceder como anteriormente se explicó, veamos un ejemplo

Tangram Ortogonal (8 piezas)

   Para comenzar la construcción debemos trazar primeramente un octógono regular. Puedes elegir la forma de hacerlo, pero a continuación desarrollamos una forma bastante sencilla, en ella no se utiliza el transportador. 

1) Traza una circunferencia y en ella, dos diámetros perpendiculares

2) Traza dos cuerdas que unan los extremos de los diámetros marcados

3) Determina el punto medio de las cuerdas marcadas anteriormente. Traza un segmento que pase por el punto antes mencionado y la intersección de los diámetros (marcados en color rojos).

4) De esta manera obtenemos los ocho puntos que serán los vértices del octógono regular   

   Luego de obtener el octógono, eliminamos todos los trazos auxiliares.

   Para facilitar la visualización de los trazos, enumeraremos los vértices de la figura.

   Siempre es recomendable reproducir la figura sobre una superficie rígida, como puede ser un cartón o plástico 

   Te dejamos algunas ideas para que reproduzcas, y al mismo tiempo te alentamos a que inventes las propias 

Tangram Circular (10 piezas)

 

   Si deseas comenzar a jugar puedes imprimir la imagen que se encuentra a continuación, o realizar la construcción tu mismo ya que es sumamente sencilla.   

1- Trazar dos rectas perpendiculares A y B   

2- Con centro en la intersección de ambas rectas trazar un circulo, quedando dos diámetros A y B

3- Marcar las cuartas partes de una de las diagonales (A)

4- Trazar un rombo, con los 1/4 del diámetro A y el  punto intersección entre el otro diámetro  B y la circunferencia

5- Marca una recta paralela a la diagonal B y que pasa por el cuarto del diámetro A

Algunas de las figuras que puedes intentar construir 

No te apresures a mirar las soluciones. Intenta reproducirlas sin hacer trampa 

   Vas a poder observar que se encontraras los mismos diseños que los presentados anteriormente 

   

Tangram Circular (9 piezas)

   En varias oportunidades hemos abordado diversos juegos. Ellos además de brindarnos la posibilidad de divertirnos, nos permiten repasar diversos conceptos o habilidades.

   En esta oportunidad les presento un Trangram circular, el cual nos permitirá representar diversas figuras sumamente armónicas.

   Luego de recortar las piezas que forman la figura; la consigna es: reproducir las figuras que se encuentran a continuación, recordando que no se pueden superponer las piezas y al mismo tiempo deben ser utilizadas todas.

   Como siempre te decimos no te preocupes si al principio no logras resolverlo, todo es practica; y para que no te desesperes . . . te dejamos las respuestas.

La Divina Proporción

     Este concepto matemático sumamente antiguo está íntimamente ligado al arte. 

     Pero al mismo tiempo al crecimiento de las plantas, animales o nuestros propios cuerpos.

     Tan importante es este concepto, que diversos autores le han dedicado años de su vida a su estudio y enseñanza.

     A continuación presentamos un poema que le han dedicado

     A LA DIVINA PROPORCIÓN

A ti, maravillosa disciplina,

media, extrema razón de la hermosura

que claramente acatas la clausura

viva en la malla de tu ley divina.

A ti, cárcel feliz de la retina,

áurea sección, celeste cuadratura,

misteriosa fontana de mesura

que el universo armónico origina.

A ti, mar de los sueños angulares,

flor de las cinco formas regulares,

dodecaedro azul, arco sonoro.

Luces por alas un compás ardiente.

Tu canto es una esfera transparente.

A ti, divina proporción de oro.

RAFAEL ALBERTI

Extraído de: "La Divina Proporción" de Luca Pacciolli