En esta oportunidad abordaremos el tema Sistemas de Ecuaciones de una manera diferente, dado que en álgebra lineal hay un teorema que permite calcular el número de soluciones de un sistema en función del rango de la matriz de coeficientes y del rango de la matriz ampliada asociadas al sistema que se esta analizando.
Dicho teorema lleva el nombre del matemático francés Eugène Rouché quien lo enunció y del matemático alemán Ferdinand George Frobenius quien fue uno de los muchos matemáticos que lo demostraron. Es por esto, que en otros idiomas recibe otros nombres; por mencionar algunos: teorema de Rouché-Capelli, teorema de Rouché-Fontené, el teorema de Kronecker-Capelli, etc.
A grandes rasgos, el teorema establece que para que un sistema de ecuaciones lineales sea compatible es condición necesaria y suficiente que la matriz formada por los coeficientes junto con la ampliada por los términos independientes posean el mismo rango; además si el rango antes mencionado es igual al número de incógnitas será compatible determinado ó será indeterminado si el rango es menor a la cantidad de incógnitas y por último será indeterminado cuando el rango de ambas matrices sea distinto entre ellos.
En el siguiente power se presentan los aspectos más importantes de este teorema. Así mismo se presentan diversos ejemplos con dos y tres incógnitas, a la vez que se presentan los sistemas en 2 y 3 dimensiones.
De esta manera se busca unir al álgebra con la geometría, dado que en aspectos tan abstractos como este, es necesario buscar una manera más sencilla de presentarlos.
queda determinado por un par de números reales: su parte real, 
y su parte imaginaria, 
. De esta manera, el par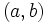 
representa las coordenadas de un punto del plano. 
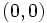y extremo 
